The fans are tested for field performance by measurement of flow, head, temperature on the fan side and electrical motor kW input on the motor side.
Air flow measurement
Static pressure
Static pressure is the potential energy put into the system by the fan. It is given up to friction in the ducts and at the duct inlet as it is converted to velocity pressure.At the inlet to the duct, the static pressure produces an area of low pressure (see Figure 1.1).
Velocity pressure
Velocity pressure is the pressure along the line of the flow that results from the air flowing through the duct. The velocity pressure is used to calculate air velocity.
Total pressure
Total pressure is the sum of the static and velocity pressure. Velocity pressure and static pressure can change as the air flows though different size ducts accelerating and de-accelerating the velocity.
The total pressure stays constant, changing only with friction losses. The illustration that follows shows how the total pressure changes in a system. The fan flow is measured using pitot tube manometer combination, or a flow sensor (differential pressure instrument) or an accurate anemometer. Care needs to be taken regarding number of traverse points, straight length section (to avoid turbulent flow regimes of measurement) up stream and downstream of measurement location.The measurements can be on the suction or discharge side of the fan and preferably both where feasible.

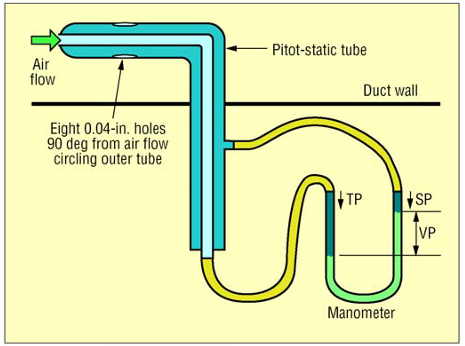
Measurement by Pitot tube
The Figure 1.2 shows how velocity pressure is measured using a pitot tube and a manometer. Total pressure is measured using the inner tube of pitot tube and static pressure is measured using the outer tube of pitot tube. When the inner and outer tube ends are connected to a manometer, we get the velocity pressure. For measuring low velocities, it is preferable to use an inclined tube manometer instead of U tube manometer.
Measurements and Calculations
Velocity pressure/velocity calculation
When measuring velocity pressure the duct diameter (or the circumference from which to calculate the diameter) should be measured as well. This will allow us to calculate the velocity and the volume of air in the duct. In most cases, velocity must be measured at several places in the same system
The velocity pressure varies across the duct. Friction slows the air near the duct walls, so the velocity is greater in the center of the duct. The velocity is affected by changes in the ducting configuration such as bends and fan curves. The best place to take measurements is in a section of duct that is straight for at least 3-5 diameters after any elbows, branch entries or duct size changes

To determine the average velocity, it is necessary to take a number of velocity pressure readings across the cross-section of the duct. The velocity should be calculated for each velocity pressure reading, and the average of the velocities should be used. Do not average the velocity pressure; average the velocities.For round ducts over 6 inches diameter, the following locations will give areas of equal concentric area (see Figure 1.3).
For best results, one set of readings should be taken in one direction and another set at a 90 ° angle to the first. For square ducts, the readings can be taken in 16 equally spaced areas. If it is impossible to traverse the duct, an approximate average velocity can be calculated by measuring the velocity pressure in the center of the duct and calculating the velocity. This value is reduced to an approximate average by multiplying by 0 .9. Air density calculation The first calculation is to determine the density of the air. To calculate the velocity and volume from the velocity pressure measurements it is necessary to know the density of the air. The density is dependent on altitude and temperature.
Gas Density(γ)=(273*1.293)/(273+t° C)
toC – temperature of gas/air at site condition
Velocity calculation
Once the air density and velocity pressure have been established, the velocity can be determined from the equation:
Velocity v,m/s =( Cp×√(2×9.81×∆p×γ))/γ
Cp = Pitot tube constant, 0.85 (or) as given by the manufacturer
∆p= Average differential pressure measured by pitot tube by taking measurement at number of points over the entire cross section of the duct.
γ= Density of air or gas at test condition.
Volume calculation
The volume in a duct can be calculated for the velocity using the equation:
Volumetric flow(Q), m3/sec=Velovity,V(m/sec)×Area(m2)
Fan efficiency
Fan manufacturers generally use two ways to mention fan efficiency: mechanical efficiency (sometimes called the total efficiency) and static efficiency. Both measure how well the centrifugal fan converts horsepower into flow and pressure.
The equation for determining mechanical efficiency is:
Fan Mechanical Efficiency(η_mechnical ),%
= (Volume in m3/sec*(total pressure) in mm WC)/(102*power inpit to fan shaft in kW )×100
Fan Mechnical Efficiency(η_mechanical ),%
= (Volume in m3 ∆p(total pressure)in mm WC)/(102* power input to fan shaft in kW)
The static efficiency equation is the same except that the outlet velocity pressure is not added to the fan static pressure
Fan Static Efficiency(η_static ),%
=(Volume in m3 /sec* ∆p(Static preesure)in mmWC)/(102* power input to fan shaft in kW)×100
Drive motor kW can be measured by a load analyzer. This kW multiplied by motor efficiency gives the shaft power to the fan.
Related Posts:
Factors Affecting Fan Performance
Air density is a variable of elevation and temperature, and both these variables affect fan air performance. Air density will affect the total pressure that a fan can generate and the horsepower required to move the air…
Fan Performance Evaluation and Efficient System Operation System Characteristics
The term “system resistance” is used when referring to the static pressure. The system resistance is the sum of static pressure losses in the system.The system resistance is…
