A centrifugal blower impeller have backward swept blades, radial tipped blades or forward swept blades as shown in figure: 1.1 below. The inlet and outlet velocity triangles are also shown accordingly in the figure. Under ideal conditions, the directions of the relative velocity vectors Vr1 and Vr2 are same as the blade angles at the entry and the exit. A zero whirl at the inlet is assumed which results in a zero angular momentum at the inlet. The backward swept blades are employed for lower pressure and lower flow rates. The radial tipped blades are employed for handling dustladen air or gas because they are less prone to blockage, dust erosion and failure. The radial-tipped blades in practice are of forward swept type at the inlet. The forward-swept blades are widely used in practice. On account of the forward-swept blade tips at the exit, the whirl component of exit velocity Vw2 is large which results in a higher stage pressure rise .
Vw2 < U2, if β2 < 900 , backward swept blades
Vw2 = U2, if β2 = 900 , radial blades Vw2 > U2, if β2 >900 , forward swept blades.
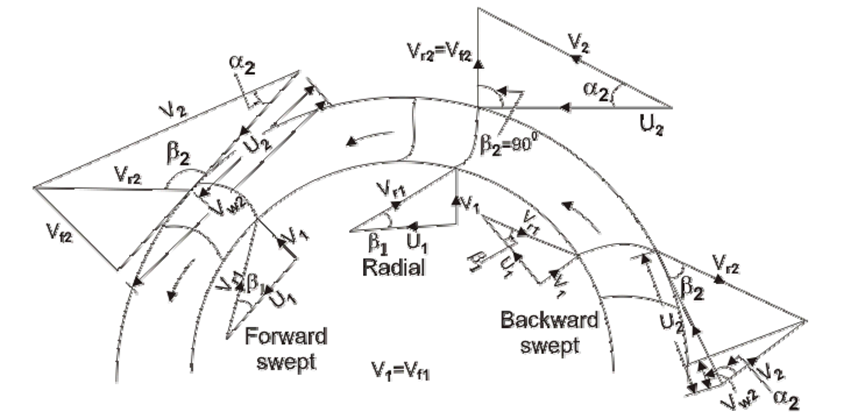
Figure: 1.1 Velocity triangles at inlet and outlet of different types of blades of an impeller of a centrifugal blower.
THEORETICAL PRESSURE DEVELOPED BY A CENTRIFUGAL IMPELLER
The theoretical pressure developed by the impeller, is achieved by using Euler’s Equation. In fluid dynamics, the Euler equations are a set of equations governing in viscid flow. They are named after Leonard Euler. The equations represent conservation of mass (continuity), momentum and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically, only the continuity and momentum equations have been derived by Euler.
The static pressure rise through the impeller is due to the change in centrifugal fan and the diffusion of relative velocity component. Therefore, it can be written as
p2 -p1 = (∆p) =1/2ρ (U2 2 -U1 2 ) + 1/2ρ (Vr1 2 -Vr2 2 )(1.1)
The stagnation pressure rise through the stage can also be obtained as
(∆p0)=1/2ρ (U2 2 -U1 2 ) + 1/2ρ (Vr1 2 -Vr2 2 ) + 1/2*ρ (V2 2 -V1 2)(1.2)
Where, U1 and U2 are peripheral velocities and V1 and V2are absolute velocities at inlet and outlet From equations (1.1) and (1.2) we get
(∆p0) = (∆p) + 1/2*ρ (V2 2 -V1 2 ) (1.3)
SLIP FACTOR The slip factor is a vital piece of information needed for the designers (also by designers of radial turbines) as its accurate estimation enables the correct value of the energy transfer between impeller and the fluid. Various attempts to determine the values of slip factor have been made and numerous research papers concerned solely with this topic have been published. Wiesner (1967) has given an extensive review of the various expressions used for determining slip factors. Most of the expressions derived relate to radially vaned impellers or to mixed flow designs, but some are given for backward swept vane designs. All of these expressions are derived from inviscid flow theory even though the real flow is far from ideal.
However, despite this lack of realism in the flow modeling, the fact remains that good results are still obtained with the various theories.
Under the ideal (frictionless) conditions the relative flow leaving the impeller of a industrial air blower will receive less than perfect guidance from the vanes and the flow is said to slip. If the impeller could be imagined as being made with an infinite number of infinitesimally thin vanes, then an ideal flow would be perfectly guided by the vanes and would leave the impeller at the vane angle. But, the relative eddy causes the flow in the impeller passages to deviate from the blade angle β2 at the exit to an angle β’2. This deviation is being larger for a larger blade pitch or for smaller number of impeller blades. On account of this effects the apex of the actual velocity triangle at the impeller exit is shifted away (opposite to the direction of the rotation) from the apex of the ideal velocity triangle. This phenomenon is known as slip and the shift of the apex is the slip velocity. It may be seen that on account of the slip the whirl component is reduced which in turn decreases the energy transfer and the pressure developed . Figure: 1.2 compares the relative flow angle β2, obtained with a finite number of vanes, with the vane angle, β’2. A slip factor may be defined as ratio of actual and ideal values of the whirl components at the exit.
µ = Vu2’ / Vu2 (1.4)
Where μ = slip factor
Vu2 = ideal exit velocity peripheral component
Vu2’ = actual exit velocity peripheral component due to slip

Figure: 1.2 Slip Factor
V = absolute velocity of fluid
Vm = meridional velocity component
Vu = peripheral velocity component
U = peripheral velocity of impeller
W = relative velocity β = blade angle
Related Posts:
In parallel side walls , the type of volute casing the sides of the casing are parallel as shown in figure: 1.2. The width of the casing is nearly kept equal to the width of the impeller.r. With most ventilation blowers …
1) All parts of the fan in contact with the air or gas being handled shall be made of nonferrous material. Steps must also be taken to assure that the impeller, bearings, and shaft are adequately attached…
