Select Fans Using Fan Total Pressure to Save Energy

The requirements for attaining a minimum level of fan energy efficiency and keeping the fan selection with an operating point close to the fan peak energy efficiency are being addressed in a recommendation for continuous maintenance proposal for ASHRAE/IES Standard 90.1. The proposal for this recommendation was made by ASHRAE Technical Committee 5.1, Fan Design and Application, and AMCA International.

In this article we focus on improving fan selection by discussing two important issues relating to reduction of the energy consumption. The first, most lucrative, is the selection of the fan so that the operating point is close to the peak fan efficiency. The second is to use fan total pressure instead of fan static pressure for fan selection. This means we must deal with a history several centuries old.

The first documented discussion of fans (devices using a bladed impeller creating a flow of air by means of rotation powered by a mechanical source) is a publication reviewing the achievements in mining and metallurgical processes from the earliest times until the 16th century.1 Bernoulli’s principle was published in 1738, and at that time fan output was defined as static pressure that was meant to refer to local static pressure. The adjective “fan” could not have been used. Much later, the terms “fan total pressure” and “fan static pressure”2 were introduced.

Partly because of this history, the long-standing practice in the United States has been to use static pressure as the basis for fan system design and selection. This practice is incorrect and often leads to consumption of significant excess energy. This article presents techniques for fan selection based on the use of total pressure and compares those results to those obtained using static pressure.

Why Fan Total Pressure?

The purpose of any air-handling system is to provide air movement to ensure the comfort and safety of the occupants of the space. Notice the keyword “movement,” which indicates why using static (defined as lacking motion) pressure is incorrect. It is the movement of the air that is important. To provide the energy required to move the air, we must produce a pressure differential favoring motion in the desired direction.

Normally, the air is confined to move through ducts or spaces by the boundaries of these ducts or spaces. Resistance to this motion is caused by friction along the boundaries and by the energy lost in components that are intended to change some property of the air (such as filters, coils, sound attenuators and grills). When the system resistance is plotted as total pressure vs. distance, the total pressure will be decreasing everywhere except across the fan. Therefore, every non-fan component will have a total pressure loss associated with it. Special attention must be paid to those components in which a large or abrupt change in cross-section occurs, since the total pressure losses can be quite large. The long-standing practice of using static pressure leads to the use of misleading terms such as “static regain” or “static pressure recovery” to describe what is actually “conversion of velocity pressure to static pressure.”

Achieving the design parameters of air-handling systems is becoming more and more important to the owners of the properties equipped with these systems. Monitoring of fan system performance is required to confirm proper operation. Using measurement of static pressure on the duct wall upstream and downstream of the fan for this purpose is useless and only creates confusion in evaluating the operational performance of an air-handling system.

The duct design chapter in the 2005 ASHRAE Handbook— Fundamentals (Chapter 35) makes it clear that the resistance to airflow in a duct system is noted by the slope of the total pressure vs. distance curve. Therefore, the loss in any fitting, length of duct or component is the change (always a decrease) in total pressure across the component. Once duct sizes are known, the static pressure at any point may be calculated from the total pressure and flow. Results of a duct design will then be a plot (or table) of total pressure vs. distance. The negative total pressure at the fan inlet can be determined after the design value(s) of the inlet total pressure are established. The total pressure difference between the fan outlet and the system outlet is known from the duct system design. The positive total pressure required at the fan outlet can be determined once the design value(s) of the outlet total pressure is established. The fan total pressure is merely the algebraic sum of the fan inlet and outlet values.

The common term “total static pressure” is clearly an oxymoron. It is used to identify the sum of the static pressure losses in the duct system, and, therefore, often used to define the fan performance requirement. Such a practice is not only dangerous, it is incorrect. As noted earlier, all losses in ducts, fitting and other components are total pressure losses. It is true that, for any fitting or component that does not include a change in flow area, the static pressure loss and the total pressure loss are equal. This is not true of fittings or components, which involve an area change, such as diffusers and wye fittings.

As we shall see in the next section, if the system resistance is (correctly) stated as total pressure vs. flow, it is critically important that this requirement is matched to the fan performance stated as total pressure vs. flow.

Fans and Pressures

A fan is a device designed to primarily deliver flow, usually of air, at relatively low pressure. The fan has an inlet opening for air to enter the fan and an outlet opening for air to leave the fan. The flow through these openings is the same and creates a velocity in each of these openings. The motor, usually an electromotor, delivers energy to the fan impeller and the impeller transforms the energy into the energy in the air handled by the fan.

If we define control surfaces at the inlet and outlet openings, the energy in the air delivered by the fan is the difference between the energy of the air in the outlet opening minus the energy in the air in the inlet opening of the fan. This energy has two components, static and dynamic. Since the flow is equal for both inlet and outlet, we may define the energy addition by the change in pressure between the two openings. The fan total pressure is then defined as the difference of the total pressures in the fan outlet and inlet openings.

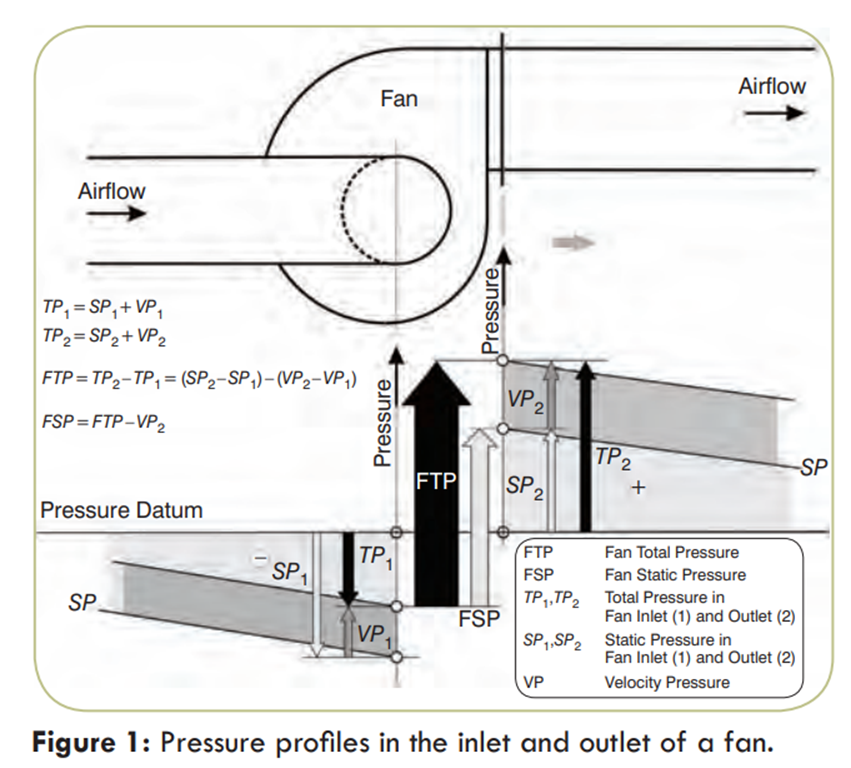
The relations among these pressures are depicted in Figure 1.

These pressures are defined in ISO 5801 and ANSI/AMCA Standard 210-07/ANSI/ASHRAE 51- 07, Laboratory Methods of Testing Fans for Certified Aerodynamic Performance Rating. Any other terms such as total static pressure, external static pressure and external total static pressure are not defined and, therefore, should not be used.
The fan static pressure as it is defined generally cannot be measured by fan testing except for a fan having the same air velocity in its inlet and outlet openings. In such case, the fan static pressure is equal to the static pressure rise across the fan.

Using Fan Static Pressure for Fan Selection

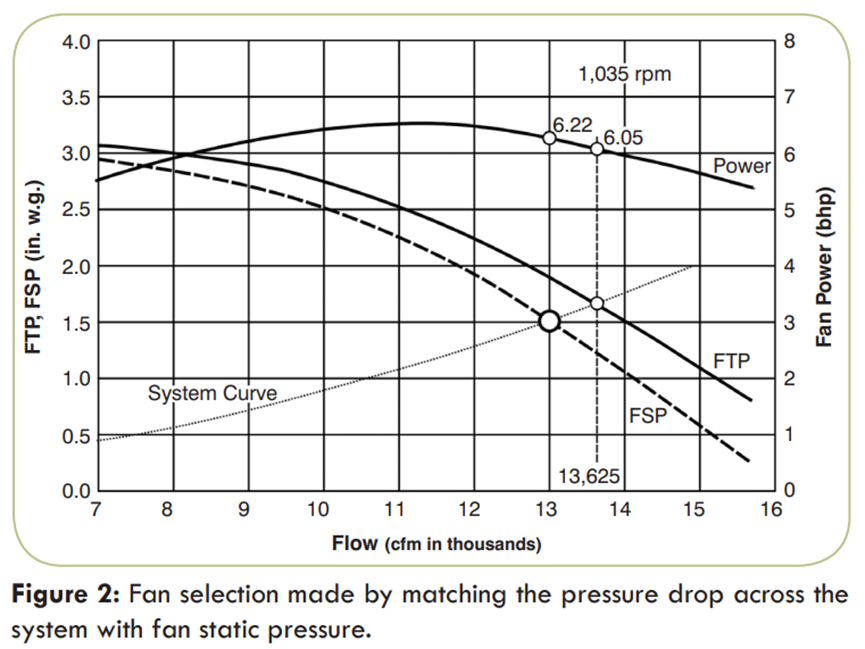
First, we must stress that the fan performance is usually presented in terms of FTP vs. flow or FSP vs. flow. In Figures 2 and 3 both presentations are used simultaneously for a typical utility centrifugal fan size 24 in. (0.6 m). The requested operating point of the system is 13,000 cfm (6135 L/s) at 1.5 in. w.g. (374 Pa) pressure at standard air density.

In Figure 2 the system pressure drop has been matched with FSP, and it was found that the fan speed would be 1,035 rpm, and the fan would need a power of 6.22 bhp (4.64 kW). But, in reality, the fan at that speed would operate at a flow of 13,625 cfm (6430 L/s) at a system pressure drop of 1.65 in. w.g. (411 Pa) The flow in the system is about 5% higher, and the power need is 6.05 bhp (4.51 kW).

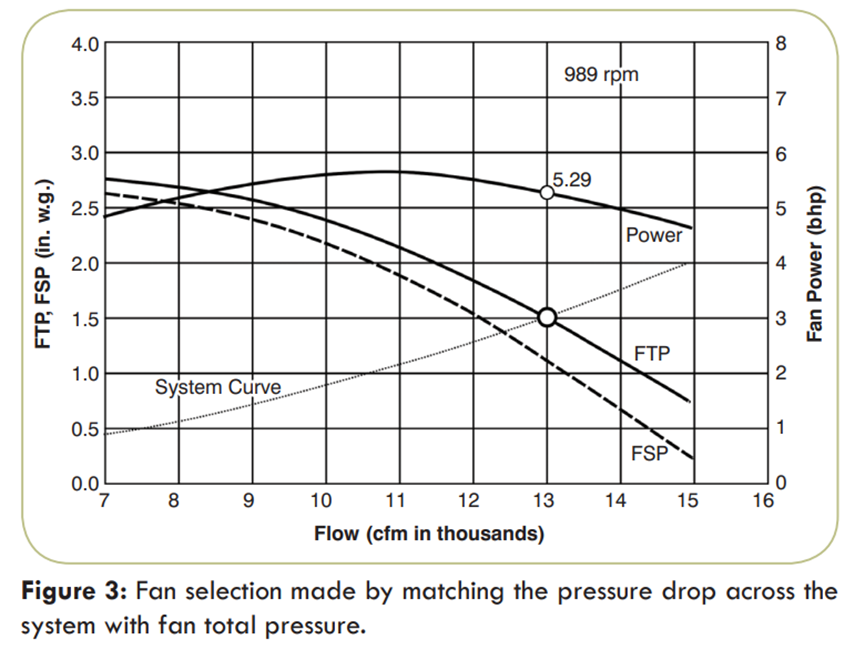
In Figure 3 the system pressure drop has been matched with FTP, and it was found that the fan speed is 989 rpm, and the fan would need a power of 5.29 bhp (3.95 kW). The flow now matches the requirement, the fan speed is down by almost 5%, and the power is down by 12.5%.

The benefits of the correct match are lower fan speed, lower sound and significantly lower power.

We can see that the selection of fans must be done by matching the fan performance (total pressure vs. flow) with the system requirement. The fan manufacturer present performance data in the form of multi-rating tables, which include values of flow, static pressure, speed and power. Conversion of these data to total pressure is simple (the velocity pressure is calculated from the flow and outlet area), but it is assumed that the connection of the fan to the system is such that the conversion of velocity pressure to static pressure at the outlet of the fan is identical to the conversion experienced in the test set-up from which the data were derived. The use of total pressure makes this assumption obvious, while the use of static pressure for selection, while matching the flow to the required value, does not call into question the validity of the selection.

The fan total pressure is simply the difference between the total pressure at the outlet and the total pressure at the inlet. Fan static pressure is defined to be fan total pressure minus the outlet velocity pressure. Equating the fan static pressure to the “total static pressure” will not result in a proper selection.

As an example, consider a blow-through system using a pair of axial fans whose outlets are connected to a plenum containing a collection of coils, filters and sound attenuators. The plenum is 7 ft high by 14 ft wide (2 m high by 4 m wide) and at the desired flow of 150,000 cfm (70 792 L/s) the sum of the total pressure losses from the inlet of the plenum to the system discharge is 8 in. w.g. (1992 Pa) with density of 0.075 lbs/ft2 (0.03 kg/m2). (In many cases the total pressure losses and the static pressure losses will be equal, and in that case it is permissible to simply sum the static pressure losses.) A 48 in. (1 m) diameter fan operating at 4 pole speed (1,780 rpm) is a reasonable selection using an expansion cone between the outlet and the plenum. The total pressure the fan must develop at 75,000 cfm (35 396 L/s) to produce a fan static pressure of 8 in. (1992 Pa) is 10.6 in. w.g. (2639 Pa). If, however, it is assumed that the fan plus cone is a unit, the total pressure required to produce a fan static pressure is 9.04 in. w.g. (2250 Pa). This difference represents a 3.1 degree change in blade angle.

Related Posts